https://school.programmers.co.kr/learn/courses/30/lessons/258705
프로그래머스
SW개발자를 위한 평가, 교육, 채용까지 Total Solution을 제공하는 개발자 성장을 위한 베이스캠프
programmers.co.kr
문제분석

n이 주어지면 밑변이 n+1로 깔림. 그리고 tops 배열에 따라 위에 삼각형이 있는지 없는지 결정된다. 1이면 위에 있는거고 0이면 없는거고 즉 위의 이미지는 일부러 짤랏지만 [0,1]이겟쥬?
그런데 삼각형 2개로 이루어진 사다리꼴과 삼각형 1개로 배치해서 가득 채우는 경우를 10007로 나누라고 한다.
문제접근
에? 이렇게 큰 수로 나눠? 이건 DP네~! 자 여기까지 감을 잡았다.
// 그런데 기존의 DP와 다른게 n도 달라질수 있고 tops에 따라 케이스가 또 달라진다
// n -> 1 tops 0 => 3개 . tops 1 => 1 +3 ==> 7
// n -> 2 tops 0 0 -> 1+4 + 2 = 7, tops 0 1 -> 1 + (4+1) + 5
// n -> 2 tops 1 0 -> 1 + (4+1) + 5 tops 1 1 -> 1 + (3+)..
뭔가 이렇게 무식하게 아카이빙하는게 맞는가..하다가 아닌거 같아서 고민을 하다 결국 솔루션을 보았다.. 못품 지능이슈였다.
https://tech.kakao.com/posts/610
2024 카카오 겨울 인턴십 코딩테스트 문제해설 - tech.kakao.com
안녕하세요, 카카오에서 계정시스템 개발을 맡고 있는 잭입니다. 2024 카카오 채...
tech.kakao.com
카카오 공식 풀이를 보면 어차피 마름모를 만들려면 아래를 가리키는 삼각형과 위를 가리키는 삼각형 각각 1개씩합쳐져서 만들어야 하는것에 집중을 하였다. 저 삼각형들의 집합을 잘보면 아래로 가리키는 것은 n개이고 위를 가리키는 삼각형은 n+1이다. 그래서 이 아래방향을 어떻게 채울지를 결정하고 나머지는 그냥 하나짜리 삼각형으로 채우는 경우를 다 구하면 어차피 정답이 된다.(위아래가 합쳐져야 어차피 마름모이기에)
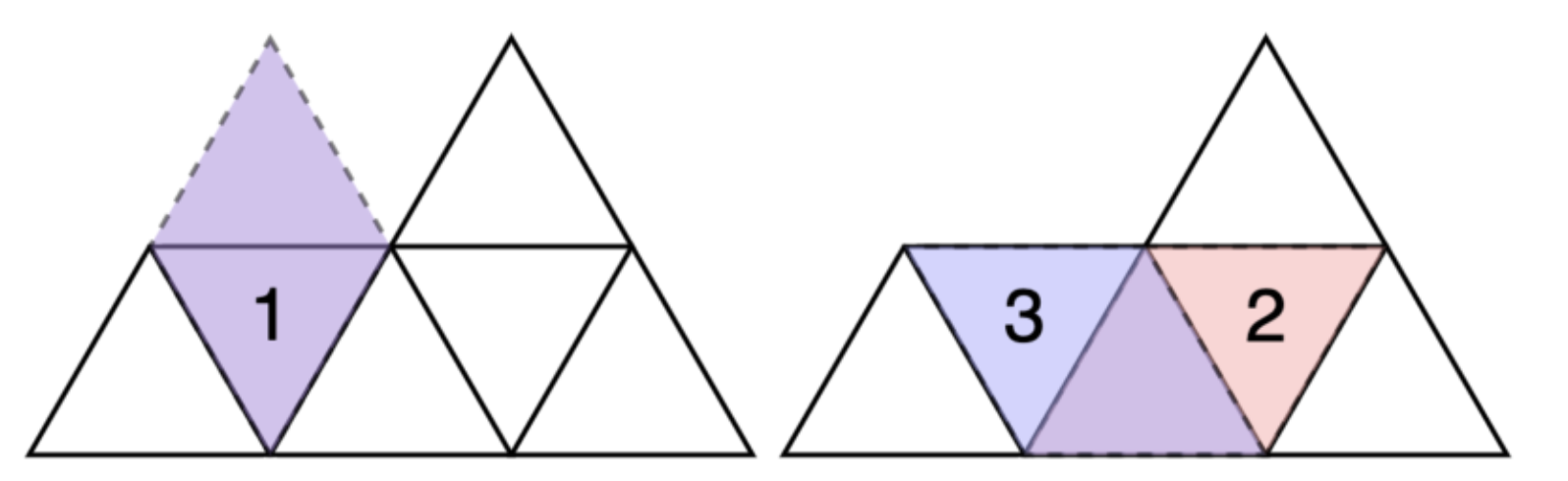
아래를 채우는 경우는 총 4가지이다.
1. 위아래 2. 왼쪽에 위가리키는 거 놓는 경우 3. 오른쪽에 위가리키는거 놓는 경우 4. 그냥 하나짜리
여기에는 제한조건이 존재한다. 1번의 경우 무조건 인덱스의 값이 1이여야한다. 또한 2의 경우 직전의 아래가리키는것이 3번이였다면 불가하다.
그래서 두가지 배열을 만들어야한다.
a[k] = k 번째 아래 방향삼각형까지 덮되, k번째아래가 3번인 경우
b[k] = k번째 아래 방향삼각형까지 덮되, k번째아래가 3번이 아닌경우
또한 tops에 0인지 1인지 두가지에 따라 다르게 해야한다.
- 1이여서 위에가 있을때
- a[k]는 k-1이 3번이든 아니든 3번 방법을 적용할 수 있다. 그래서 a[k] = a[k-1] + b[k-1]
- b[k]는 k-1이 3번이다? 그러면 2번 못하죠 즉 1 or 4번만 ㄱㄴ. k-1이 3이 아니다? 1 or 2 or 4 ㄱㄴ
- 그래서 b[k] = a[k-1] * 2 + b[k-1] * 3이 된다.
- 0이여서 위에가 없을때
- a[k] = a[k-1] + b[k-1]
- b[k]는 1번 사용 불가. 그래서 a[k-1] + b[k-1] * 2
코드
import Foundation
func solution(_ n:Int, _ tops:[Int]) -> Int {
var adp = Array(repeating: 0, count: n+1) // 3번방법만
var bdp = Array(repeating: 0, count: n+1) // 3번빼고
adp[1] = 1
bdp[1] = tops[0] == 1 ? 3 : 2
if n == 1 {
return adp[1] + bdp[1]
}
for i in 2..<n+1 {
if tops[i-1] == 0 {
adp[i] = adp[i-1] + bdp[i-1]
bdp[i] = adp[i-1] + 2 * bdp[i-1]
} else {
adp[i] = adp[i-1] + bdp[i-1]
bdp[i] = 2 * adp[i-1] + 3 * bdp[i-1]
}
adp[i] %= 10007
bdp[i] %= 10007
}
return (adp[n] + bdp[n]) % 10007
}dp 시간복잡도 n
'알고리즘' 카테고리의 다른 글
| 22968-균형(swift풀이) (0) | 2024.12.26 |
|---|---|
| 12980좋아하는 수열 - swift (14) | 2024.11.13 |
| 상담원인원-Swift풀이 (1) | 2024.11.12 |
| 17298-Swift백준골드4 (3) | 2024.10.08 |
| 9251-Swift알고리즘 (1) | 2024.03.17 |